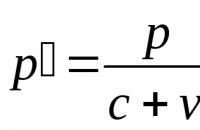În general, un sistem automat constă dintr-un obiect de control și un set de dispozitive care asigură controlul acestui obiect. De regulă, acest set de dispozitive include dispozitive de măsurare, dispozitive de amplificare și conversie, precum și dispozitive de acționare. Dacă combinăm aceste dispozitive într-o singură legătură (dispozitiv de control), atunci diagrama bloc a sistemului arată astfel:

Într-un sistem automat, informațiile despre starea obiectului controlat sunt furnizate la intrarea dispozitivului de control printr-un dispozitiv de măsurare. Astfel de sisteme se numesc sisteme de feedback sau sisteme închise. Absența acestei informații în algoritmul de control indică faptul că sistemul este deschis. Vom descrie starea obiectului de control în orice moment variabile
, care se numesc coordonate de sistem sau variabile de stare. Este convenabil să le considerați coordonate - vector de stare dimensională.

Dispozitivul de măsurare oferă informații despre starea obiectului. Dacă se bazează pe măsurarea vectorială
pot fi găsite valorile tuturor coordonatelor
vector de stare
, atunci se spune că sistemul este complet observabil.

Dispozitivul de control generează o acțiune de control
. Pot exista mai multe astfel de acțiuni de control pe care le formează - vector de control dimensional.

Intrarea dispozitivului de control primește o intrare de referință
. Această acțiune de intrare conține informații despre starea obiectului. Obiectul de control poate fi supus unei influențe perturbatoare
, care reprezintă o sarcină sau o perturbare. Măsurarea coordonatelor unui obiect se realizează de obicei cu unele erori
, care sunt de asemenea aleatoare.

Sarcina dispozitivului de control este de a dezvolta o astfel de acțiune de control
astfel încât calitatea funcționării sistemului automat în ansamblu ar fi cea mai bună într-un anumit sens.

Vom lua în considerare obiectele de control care sunt gestionabile. Adică, vectorul de stare poate fi modificat după cum este necesar prin schimbarea corespunzătoare a vectorului de control. Vom presupune că obiectul este complet observabil.

De exemplu, poziția unei aeronave este caracterizată de șase coordonate de stat. Acest
- coordonatele centrului de masă,
- Unghiurile Euler, care determină orientarea aeronavei în raport cu centrul de masă. Atitudinea aeronavei poate fi modificată folosind ascensoare, direcție, eleron și vectoring de tracțiune. Astfel, vectorul de control este definit după cum urmează:

- unghiul de deviere a liftului

- bine

- eleron

- tractiune

Vector de stare
în acest caz, se definește după cum urmează:

Puteți pune problema selectării unui control cu ​​ajutorul căruia aeronava este transferată dintr-o stare inițială dată
la o stare finală dată
cu un consum minim de combustibil sau într-un timp minim.

Complexitatea suplimentară în rezolvarea problemelor tehnice apare datorită faptului că, de regulă, se impun diverse restricții asupra acțiunii de control și asupra coordonatelor de stare ale obiectului de control.

Există restricții cu privire la orice unghi al elevatoarelor, viciilor și eleronelor:

- tracțiunea în sine este limitată.

Coordonatele de stare ale obiectului de control și derivatele acestora sunt, de asemenea, supuse unor restricții care sunt asociate cu supraîncărcările permise.

Vom lua în considerare obiectele de control care sunt descrise de ecuația diferențială:

(1)

Sau sub formă vectorială:

--vector dimensional al stării obiectului

--vector dimensional al acţiunilor de control

- funcția părții drepte a ecuației (1)

La vectorul de control
se impune o restricție, vom presupune că valorile acesteia aparțin unei regiuni închise unele -spațiul dimensional. Aceasta înseamnă că funcția executivă
aparține regiunii în orice moment (
).

Deci, de exemplu, dacă coordonatele funcției de control satisfac inegalitățile:

apoi zona este -cub măsurat.

Să numim orice funcție continuă pe bucăți un control admisibil
, ale căror valori în fiecare moment de timp aparține regiunii , și care poate avea discontinuități de primul fel. Rezultă că și în unele probleme de control optim soluția poate fi obținută în clasa controlului continuu pe bucăți. Pentru a selecta controlul
în funcţie de timp şi starea iniţială a sistemului
, care determină în mod unic mișcarea obiectului de control, se cere ca sistemul de ecuații (1) să îndeplinească condițiile teoremei de existență și unicitate a soluției în regiune.
. Această zonă conține posibile traiectorii ale mișcării obiectului și posibile funcții de control.
. Dacă domeniul de variabile este convex, atunci pentru existența și unicitatea unei soluții este suficient ca funcția

. au fost continue în toate argumentele și au avut derivate parțiale continue cu privire la variabile

.

Ca criteriu care caracterizează calitatea funcționării sistemului, este selectat un funcțional al formei:

(2)

Ca functie
vom presupune că este continuă în toate argumentele sale și are derivate parțiale continue în raport cu

.

În ultimii ani, managementul optim a început să fie utilizat atât în ​​sistemele tehnice pentru îmbunătățirea eficienței proceselor de producție, cât și în sistemele de management organizațional pentru îmbunătățirea activităților întreprinderilor, organizațiilor și sectoarelor economiei naționale.

În sistemele organizaționale, cineva este de obicei interesat de rezultatul final, stabilit al echipei, fără a explora

eficiența în timpul procesului de tranziție între emiterea unei comenzi și obținerea rezultatului final Acest lucru se explică prin faptul că, de obicei, în astfel de sisteme pierderile în procesul de tranziție sunt destul de mici și nu afectează semnificativ câștigul general în starea de echilibru, deoarece starea de echilibru în sine este mult mai lungă decât procesul de tranziție. Dar uneori dinamica nu este studiată din cauza dificultăților matematice. Cursurile de metode sunt dedicate metodelor de optimizare a stărilor finale în sisteme organizaționale și economice. optimizare și cercetare operațională.

În controlul sistemelor tehnice dinamice, optimizarea este adesea esențială în special pentru procesele tranzitorii, în care indicatorul de eficiență depinde nu numai de valorile coordonatelor curente (ca în controlul extrem), ci și de natura schimbării din trecut. , prezent și viitor, și se exprimă prin unele funcționale asupra coordonatelor, derivatelor acestora și, poate, timpului.

Un exemplu este controlul unui atlet care alergă pe o distanță. Întrucât rezerva sa de energie este limitată de factori fiziologici, iar consumul rezervei depinde de natura alergării, sportivul nu mai poate da puterea maximă posibilă în fiecare moment, pentru a nu epuiza rezerva de energie prematur și nu. rămâne fără energie pe distanță, dar trebuie să caute modul optim de alergare pentru caracteristicile sale.

Găsirea controlului optim în astfel de probleme dinamice necesită rezolvarea unei probleme matematice destul de complexe în procesul de control folosind metodele de calcul al variațiilor sau de programare matematică, în funcție de tipul de descriere matematică (model matematic) a sistemului. Astfel, dispozitivul de calcul sau calculatorul devine o componentă organică a sistemului de control optim. Principiul este explicat în Fig. 1.10. Intrarea dispozitivului de calcul (mașină) VM primește informații despre valorile curente ale coordonatelor x de la ieșirea obiectului O, despre controale și din intrarea acestuia, despre influențele externe z asupra obiectului, precum și stabilirea diferitelor condiții din exterior: valoarea criteriului de optimitate pentru condiții la limită, informații despre valorile admisibile Calcul

6.2.1. Enunțarea și clasificarea problemelor în teoria controlului optim.În majoritatea covârșitoare a problemelor pe care le-am luat în considerare, factorii asociați cu modificările în timp ale obiectelor și sistemelor studiate au fost scoși din ecuație. Poate că, dacă sunt îndeplinite anumite condiții prealabile, o astfel de abordare este constructivă și legitimă. Cu toate acestea, este, de asemenea, evident că acest lucru nu este întotdeauna acceptabil. Există o clasă largă de probleme în care este necesar să se găsească acțiunile optime ale unui obiect, ținând cont de dinamica stărilor sale în timp și spațiu. Metodele de rezolvare a acestora fac obiectul teoriei matematice a controlului optim.

Într-o formă foarte generală, problema de control optim poate fi formulată după cum urmează:

Există un anumit obiect, a cărui stare este caracterizată de două tipuri de parametri - parametrii de stare și parametrii de control, iar în funcție de alegerea acestuia din urmă, procesul de gestionare a obiectului decurge într-un fel sau altul. Calitatea procesului de control este evaluată folosind un anumit funcțional*, pe baza căruia este stabilită sarcina: să găsească o succesiune de valori ale parametrilor de control pentru care această funcționalitate ia o valoare extremă.

* Funcționalitate este o funcție numerică ale cărei argumente, de regulă, sunt alte funcții.

Din punct de vedere formal, multe probleme de control optim pot fi reduse la probleme de programare liniară sau neliniară de dimensiuni mari, deoarece fiecare punct din spațiul de stare are propriul său vector de variabile necunoscute. Totuși, de regulă, mișcarea în această direcție fără a ține cont de specificul problemelor corespunzătoare nu duce la algoritmi raționali și eficienți pentru rezolvarea acestora. Prin urmare, metodele de rezolvare a problemelor de control optim sunt asociate în mod tradițional cu alte aparate matematice, provenite din calculul variațiilor și teoria ecuațiilor integrale. De remarcat, de asemenea, că, din nou, din motive istorice, teoria controlului optim s-a concentrat pe aplicații fizice și tehnice, iar aplicarea ei pentru rezolvarea problemelor economice este, într-un anumit sens, de natură secundară. În același timp, într-o serie de cazuri, modelele de cercetare care utilizează aparatul teoriei controlului optim pot duce la rezultate semnificative și interesante.

La cele de mai sus, este necesar să se adauge o remarcă despre legătura strânsă care există între metodele utilizate pentru rezolvarea problemelor de control optim și programarea dinamică. În unele cazuri ele pot fi folosite alternativ, iar în altele se pot completa reciproc cu succes.

Există diverse abordări pentru clasificarea problemelor de control optim. În primul rând, acestea pot fi clasificate în funcție de obiectul de control:

Ø Ø sarcini de management cu parametrii concentrați;

Ø Ø sarcini de gestionare a obiectelor cu parametrii distribuiti.

Un exemplu al primului este controlul unei aeronave în ansamblu, iar cel de-al doilea este controlul unui proces tehnologic continuu.

În funcție de tipul de rezultate la care conduc controalele aplicate, există deterministŞi stocastică sarcini. În acest din urmă caz, rezultatul controlului este un set de rezultate descrise de probabilitățile de apariție a acestora.

Pe baza naturii schimbărilor din sistemul controlat de-a lungul timpului, sarcinile se disting:

Ø Ø cu discret timpuri schimbătoare;

Ø Ø cu continuu timpuri schimbătoare.

Problemele de gestionare a obiectelor cu un set discret sau continuu de stări posibile sunt clasificate în mod similar. Problemele de control pentru sistemele în care timpul și stările se modifică discret se numesc probleme de control mașini cu stări finite. În sfârșit, în anumite condiții, pot fi puse probleme de gestionare a sistemelor mixte.

Multe modele de sisteme controlate se bazează pe aparatul de ecuații diferențiale, atât derivate ordinare, cât și derivate parțiale. La studierea sistemelor cu parametri distribuiți, în funcție de tipul de ecuații diferențiale parțiale utilizate, astfel de probleme de control optim se disting ca parabolice, eliptice sau hiperbolice.

Să luăm în considerare două exemple simple de probleme de gestionare a obiectelor economice.

Problema de alocare a resurselor. Disponibil T depozite cu numere i (i∊1:m), destinate depozitării unui produs omogen. În momente discrete în timp t∊0:(T-l) se distribuie intre obiecte de consum (clienti) cu numere j, j∊1:n. Reaprovizionarea stocului la punctele de depozitare a produselor în t- instant de timp este determinat de cantități a i t,i∊1:m, iar nevoile clienților pentru aceasta sunt egale b j t, j∊1:n. Să notăm prin c t i,j- costul livrării unei unităţi de produs din i depozitul j-al-lea consumator la timp t. De asemenea, se presupune că produsul a primit la depozit la momentul respectiv t, poate fi folosit incepand din momentul urmator ( t+l). Pentru modelul formulat, sarcina este de a găsi un astfel de plan de distribuție a resurselor ( x t i,j} Tm x n, care minimizează costurile totale de livrare a produselor către consumatori din depozite pe toată perioada de funcționare a sistemului.

Desemnat de x t i,j cantitatea de produs furnizată j-al-lea client cu i depozitul în t al-lea moment de timp și după z t i- cantitatea totală de produs per i- depozit, problema descrisă mai sus poate fi reprezentată ca problema găsirii unor astfel de seturi de variabile

care minimizează funcția

in conditii

unde este volumul stocurilor inițiale de produse din depozite z 0 i = ž i. se presupune că sunt date.

Problema (6.20)-(6.23) se numește problema de programare liniară a transportului dinamic. În ceea ce privește terminologia de mai sus, variabile independente x t i,j reprezenta parametrii de control sistem și variabilele care depind de acestea z t i- totalitate parametrii de stare sisteme la un moment dat t. Restricții z t i≥ 0 garantează că, în orice moment, un volum de produs care depășește cantitatea reală nu poate fi exportat din niciun depozit, iar restricțiile (6.21) stabilesc regulile de modificare a acestei cantități atunci când se trece de la o perioadă la alta. Constrângerile de acest tip, care stabilesc condiții pentru valorile parametrilor de stare a sistemului, sunt de obicei numite fază.

Rețineți, de asemenea, că condiția (6.21) servește ca exemplu cel mai simplu de restricții de fază, deoarece valorile parametrilor de stare pentru două perioade adiacente sunt asociate tŞi t+l. În general, se poate stabili o dependență pentru un grup de parametri aparținând mai multor etape, eventual necontigue. O astfel de nevoie poate apărea, de exemplu, atunci când se ia în considerare factorul de întârziere a livrării în modele.

Cel mai simplu model dinamic al macroeconomiei. Să ne imaginăm economia unei anumite regiuni ca un set n industrii ( j∊1:n), al cărui produs brut în termeni monetari la un moment dat t poate fi reprezentat ca un vector z t=(z t 1 , z t 2 ,..., z t n), Unde t∊0:(T-1). Să notăm prin A t matricea costurilor directe ale căror elemente a t i,j, reflectă costurile produsului i a-a industrie (în termeni monetari) pentru producerea unei unități de produs j-a industrie în t al-lea moment în timp. Dacă Xt= ║x t i,j║n x m- matrice care specifica standardele specifice de productie i-industria va extinde producția în j-a industrie, și y t = (y t 1 , y t 2 , ..., y t n) este vectorul volumelor de produse ale industriilor de consum destinate consumului, atunci condiția reproducerii extinse poate fi scrisă ca

Unde z 0 = ž - se presupune că este dat stocul iniţial de produse ale industriilor şi

În modelul luat în considerare, cantitățile z t sunt parametri ai stării sistemului și Xt- parametri de control. Pe baza acesteia, pot fi puse diverse sarcini, un reprezentant tipic al cărora este problema producției optime a economiei în acest moment. T la o anumită stare dată z*. Această problemă se rezumă la găsirea unei secvențe de parametri de control

satisfacerea conditiilor (6.24)-(6.25) si minimizarea functiei

6.2.2. Cea mai simplă problemă de control optim. Una dintre tehnicile folosite pentru rezolvarea problemelor extreme este de a izola o anumită problemă care admite o soluție relativ simplă, la care alte probleme pot fi reduse în viitor.

Să luăm în considerare așa-numitul cea mai simplă problemă de control. Ea arată ca

Specificul condițiilor problemei (6.27)-(6.29) este că funcțiile de control al calității (6.27) și restricțiile (6.28) sunt liniare în raport cu z t, în același timp funcție g(t, x t), incluse în (6.28), pot fi arbitrare. Ultima proprietate face ca problema să fie neliniară chiar și cu t=1, adică în versiunea statică.

Ideea generală de rezolvare a problemei (6.27)-(6.29) se reduce la „împărțirea” acesteia în subsarcini pentru fiecare moment individual de timp, sub presupunerea că acestea sunt rezolvabile cu succes. Să construim funcția Lagrange pentru problema (6.27)-(6.29)

unde λ t- vectorul multiplicatorilor Lagrange ( t∊0:T). Restricțiile (6.29), care sunt de natură generală, nu sunt incluse în funcția (6.30) în acest caz. Să-l scriem într-o formă puțin diferită

Condiții necesare pentru extremul funcției Ф (x, z,λ) peste un set de vectori z t sunt date de un sistem de ecuații

care se numeste sistem pentru variabile conjugate. După cum puteți vedea, procesul de găsire a parametrilor λ tîn sistemul (6.32) se efectuează recursiv în ordine inversă.

Condiții necesare pentru extremul funcției Lagrange în variabilele λ t va fi echivalent cu restricțiile (6.28) și, în sfârșit, condițiile pentru extremul său asupra unui set de vectori x t∊X t, t∊1:(T-1) trebuie găsită ca urmare a rezolvării problemei

Astfel, problema găsirii unui control optim se reduce la căutarea controalelor care sunt suspectate a fi optime, adică acelea pentru care este îndeplinită condiția de optimitate necesară. Aceasta, la rândul său, se rezumă la găsirea unor astfel de lucruri t, t, t, îndeplinind sistemul de condiții (6.28), (6.32), (6.33), care se numește Principiul maxim discret al lui Pontryagin.

Teorema este adevărată.

Dovada.

Lasă t, t, t, satisface sistemul (6.28), (6.32), (6.33). Apoi din (6.31) și (6.32) rezultă că

iar din moment ce t satisface (6.33), atunci

Pe de altă parte, în virtutea (6.28) rezultă din (6.30) că pentru orice vector t

Prin urmare,

Aplicând teorema (6.2), precum și prevederile teoriei programării neliniare referitoare la legătura dintre soluția unei probleme extreme și existența unui punct de șa (vezi secțiunea 2.2.2), ajungem la concluzia că vectorii t, t sunt soluția celei mai simple probleme de control optim (6.27)-(6.29).

Ca urmare, am primit o schemă simplă logic pentru rezolvarea acestei probleme: din relațiile (6.32) se determină variabilele conjugate. t, apoi în cursul rezolvării problemei (6.33) se găsesc controalele t iar mai departe de (6.28) - traiectoria optimă a stărilor t,.

Metoda propusă se referă la rezultatele fundamentale ale teoriei controlului optim și, după cum am menționat mai sus, este importantă pentru rezolvarea multor probleme mai complexe, care, într-un fel sau altul, sunt reduse la cele mai simple. În același timp, limitele utilizării sale eficiente sunt evidente, care depind în întregime de posibilitatea de rezolvare a problemei (6.33).

CONCEPTE-CHEIE

Ø Ø Joc, jucător, strategie.

Ø Ø Jocuri cu sumă zero.

Ø Ø Jocuri Matrix.

Ø Ø Jocuri antagoniste.

Ø Ø Principiile maximin si minimax.

Ø Ø Punctul de șa al jocului.

Ø Ø Pret joc.

Ø Ø Strategie mixtă.

Ø Ø Teorema principală a jocurilor matriceale.

Ø Ø Problemă dinamică de transport.

Ø Ø Cel mai simplu model dinamic al macroeconomiei.

Ø Ø Cea mai simplă problemă de control optim.

Ø Ø Principiul maxim discret al lui Pontryagin.

ÎNTREBĂRI DE TEST

6.1. Formulați pe scurt subiectul teoriei jocurilor ca disciplină științifică.

6.2. Care este sensul conceptului de „joc”?

6.3. Pentru a descrie ce situații economice poate fi folosit aparatul teoriei jocurilor?

6.4. Ce joc se numește antagonist?

6.5. Cum sunt definite în mod unic jocurile matrice?

6.6. Care sunt principiile maximin și minimax?

6.7. În ce condiții putem spune că un joc are un punct de șa?

6.8. Dați exemple de jocuri care au un punct de șa și cele care nu.

6.9. Ce abordări există pentru a determina strategiile optime?

6.10. Ce se numește „prețul jocului”?

6.11. Definiți conceptul de „strategie mixtă”.

REFERINȚE

1. Abramov L. M., Kapustin V. F. Programare matematică. L., 1981.

2. Ashmanov S.A. Programare liniară: manual. indemnizatie. M., 1981.

3. Ashmanov S. A., Tikhonov A. V. Teoria optimizării în probleme și exerciții. M., 1991.

4. Bellman R. Programare dinamică. M., 1960.

5. Bellman R., Dreyfus S. Probleme aplicate de programare dinamică. M., 1965.

6. Gavurin M.K., Malozemov V.N. Probleme extreme cu constrângeri liniare. L., 1984.

7. Gass S. Programare liniară (metode și aplicații). M., 1961.

8. Gail D. Teoria modelelor economice liniare M., 1963.

9. Gill F., Murray W., Wright M. Optimizare practica / Transl. din engleză M., 1985.

10. Davydov E.G. Cercetare operațională: Proc. manual pentru studenți. M., 1990.

11. Danzig J. Programarea liniară, generalizările și aplicațiile sale. M., 1966.

12. Eremin I. I., Astafiev N. N. Introducere în teoria programării liniare și convexe. M., 1976.

13. Ermolyev Yu.M., Lyashko I.I., Mikhalevich V.S., Tyuptya V.I. Metode matematice de cercetare operațională: Proc. manual pentru universități. Kiev, 1979.

14. Zaichenko Yu P. Cercetare operațională, ed. a II-a. Kiev, 1979.

15. Zangwill W.I. Programare neliniară. Abordare unificată. M., 1973.

16. Zeutendijk G. Metode de direcții posibile. M., 1963.

17. Karlin S. Metode matematice în teoria jocurilor, programare și economie. M., 1964.

18. Karmanov V. G. Programare matematică: manual. indemnizatie. M., 1986.

19. Korbut A.A., Finkelyitein Yu.Yu. Programare discretă. M., 1968.

20. Kofman A., Henri-Laborder A. Metode și modele de cercetare operațională. M., 1977.

21. Künze G.P., Krelle V. Programare neliniară. M., 1965.

22. Lyashenko I.N., Karagodova E.A., Chernikova N.V., Shor N.3. Programare liniară și neliniară. Kiev, 1975.

23. McKinsey J. Introducere în teoria jocurilor. M., 1960.

24. Mukhacheva E. A., Rubinshtein G. Sh. Programare matematică. Novosibirsk, 1977.

25. Neumann J., Morgenstern O. Teoria jocurilor și comportamentul economic. M, 1970.

26. Ore O. Teoria grafurilor. M., 1968.

27. Taha X. Introducere în Cercetarea operațională / Trans. din engleză M., 1985.

28. Fiacco A., McCormick G. Programare neliniară. Metode de minimizare secvențială necondiționată. M., 1972.

29. Hadley J. Programare neliniară și dinamică. M., 1967.

30. Yudin D.B., Golshtein E.G. Programare liniară (teorie, metode și aplicații). M., 1969.

31. Yudin D.B., Golshtein E.G. Programare liniară. Teorie și metode finale. M., 1963.

32. Lapin L. Metode cantitative pentru deciziile de afaceri cu cazuri. Ediția a patra. HBJ, 1988.

33. Liitle I.D.C., Murty K.G., Sweeney D.W., Karel C. Un algoritm de călătorie pentru problema vânzătorului ambulant. - Cercetări operaționale, 1963, vol.11, Nr. 6, p. 972-989/ rusă. traducere: Little J., Murthy K., Sweeney D., Kerel K. Algoritm pentru rezolvarea problemei vânzătorului ambulant. - În cartea: Economie și metode matematice, 1965, vol. 1, p. 94-107.

PREFAŢĂ................................................. .. ................................................ ........................................................ .............................................................. ................... ..... 2

INTRODUCERE................................................. ....... ................................................. ............................................................. ................................................... ......................... ............. 3

CAPITOLUL 1. PROGRAMARE LINEARĂ................................................ ....... ................................................. ............................................................. ...... 8

1.1. FORMULAREA PROBLEMEI DE PROGRAMARE LINEARĂ............................................... ........................ ................................ ..................... 9

1.2. PROPRIETĂȚI DE BAZĂ ALE ZLP ȘI PRIMA SA INTERPRETARE GEOMETRICĂ............................................... .......................... ................. 11

1.3. SOLUȚII DE BAZĂ ȘI A DOUA INTERPRETARE GEOMETRICĂ A ZLP............................................ .......................... ................................ ... 15

1.4. METODĂ SIMPLEX ............................................................. .... ................................................. .......................................................... .................................................. .. 17

1.5. METODA SIMPLEX MODIFICATA.................................................. ............................................................. ........... .................................... 26

1.6. TEORIA DUALITĂȚII ÎN PROGRAMAREA LINEARĂ............................................ ........................................................ 30

1.7. METODA DUAL SIMPLEX .................................................. ............................................................. .......................................................... ................. .37

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ........................ 42

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. ...... 43

CAPITOLUL 2. PROGRAMARE NELINIARĂ............................................. ....... ................................................. ............. .................................... 44

2.1. METODE DE REZOLVARE A PROBLEMELOR DE PROGRAMARE NELINIARĂ............................................ ........................................................ 44

2.2. DUALITATEA ÎN PROGRAMARE NELINIARĂ........................................................ .......................................................... ............................ ...55

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ........................ 59

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. ...... 59

CAPITOLUL 3. SARCINI DE TRANSPORT ȘI DE REȚEA............................................ ........................................................ ............................................................... 60

3.1. PROBLEMA DE TRANSPORT ȘI METODE DE SOLUȚIONARE A EI........................................... ........................................................ ............................................. 60

3.2. SARCINI DE REȚEA................................................... .................................................. .............................................. ............................ ................................ ............... 66

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ................. 73

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. ...... 73

CAPITOLUL 4. PROGRAMARE DISCRETA................................................ ....... ................................................. ............. .................................... 74

4.1. TIPURI DE SARCINI DE PROGRAMARE DISCRETE........................................... ..................... ................................ .............................................. 74

4.2. METODA GOMORI............................................................. ................................................... ........................................................ ............................................................... ........ 78

4.3. METODA RUMULUI ȘI A LĂMĂRILOR .................................................. ...................................................... ............ ................................................ ................. ........................ 81

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ................. 86

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. ...... 86

CAPITOLUL 5. PROGRAMARE DINAMICĂ............................................. ....... ................................................. ............................................. 86

5.1. SCHEMA GENERALĂ A METODELOR DE PROGRAMARE DINAMICĂ............................................... ........................ ................................ .......... 86

5.2. EXEMPLE DE PROBLEME DE PROGRAMARE DINAMICĂ............................................. ....................... ................................. ............................. .... 93

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ................. 101

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. .......... 101

CAPITOLUL 6. SCURT PREZENTARE GENERALĂ A ALTE SECȚIUNI DE CERCETARE OPERAȚIONALĂ....................................... ............ ........................ 101

6.1. TEORIA JOCURILOR ................................................ ................................................... ........................................................ ............................................................... ..................... 101

6.2. TEORIA CONTROLULUI OPTIM.................................................. ..................... ................................ .......................................................... .................... 108

CONCEPTE CHEIE................................................ ................................................... ......................... ......................... ............................... ................... ................. 112

ÎNTREBĂRI DE TEST ............................................... ................ ................................. ....................... ................................. ............................................................. .......... 112

REFERINȚE .................................................. ................. ................................ ........................ ................................ .............................................. ................ 112

Control optim

Control optim este sarcina de a proiecta un sistem care asigură, pentru un anumit obiect de control sau proces, o lege de control sau o secvență de control de influențe care asigură maximul sau minimul unui set dat de criterii de calitate a sistemului.

Pentru rezolvarea problemei de control optim se construiește un model matematic al obiectului sau procesului controlat, care descrie comportamentul acestuia în timp sub influența acțiunilor de control și a propriei stări curente. Modelul matematic pentru problema de control optim include: formularea scopului de control, exprimat prin criteriul calității controlului; determinarea ecuațiilor diferențiale sau diferențiale care descriu posibile moduri de deplasare a obiectului de control; determinarea restricţiilor asupra resurselor utilizate sub formă de ecuaţii sau inegalităţi.

Cele mai utilizate metode în proiectarea sistemelor de control sunt calculul variațiilor, principiul maxim al lui Pontryagin și programarea dinamică Bellman.

Uneori (de exemplu, la gestionarea unor obiecte complexe, cum ar fi un furnal în metalurgie sau la analizarea informațiilor economice), datele și cunoștințele inițiale despre obiectul controlat la stabilirea problemei de control optim conțin informații incerte sau neclare care nu pot fi prelucrate de către tradiționale. metode cantitative. În astfel de cazuri, puteți utiliza algoritmi de control optim bazați pe teoria matematică a mulțimilor fuzzy (controlul fuzzy). Conceptele și cunoștințele utilizate sunt convertite în formă neclară, sunt determinate reguli neclare pentru derivarea deciziilor, iar apoi deciziile neclare sunt convertite înapoi în variabile de control fizic.

Problemă de control optim

Să formulăm problema de control optim:

aici este vectorul de stare - control, - momentele inițiale și finale ale timpului.

Problema optimă de control este să găsești funcții de stare și control pentru timp care să minimizeze funcționalitatea.

Calculul variațiilor

Să considerăm această problemă de control optim ca o problemă Lagrange în calculul variațiilor. Pentru a găsi condițiile necesare pentru un extremum, aplicăm teorema Euler-Lagrange. Funcția Lagrange are forma: , unde sunt condițiile la limită. Lagrangianul are forma: , unde , , sunt vectori n-dimensionali ai multiplicatorilor Lagrange.

Condițiile necesare pentru un extremum, conform acestei teoreme, au forma:

Condițiile necesare (3-5) formează baza pentru determinarea traiectoriilor optime. După ce am scris aceste ecuații, obținem o problemă la graniță în două puncte, în care o parte din condițiile la limită este specificată la momentul inițial de timp, iar restul la momentul final. Metodele de rezolvare a unor astfel de probleme sunt discutate în detaliu în carte.

Principiul maxim al lui Pontryagin

Necesitatea principiului maxim Pontryagin apare în cazul în care nicăieri în intervalul admisibil al variabilei de control nu este posibilă îndeplinirea condiției necesare (3), și anume .

În acest caz, condiția (3) se înlocuiește cu condiția (6):

În acest caz, conform principiului maxim al lui Pontryagin, valoarea controlului optim este egală cu valoarea controlului la unul dintre capetele intervalului admisibil. Ecuațiile lui Pontryagin sunt scrise folosind funcția Hamilton H, definită prin relație. Din ecuaţii rezultă că funcţia Hamilton H este legată de funcţia Lagrange L astfel: . Substituind L din ultima ecuație în ecuațiile (3-5) obținem condițiile necesare exprimate prin funcția Hamilton:

Condițiile necesare scrise în această formă se numesc ecuații Pontryagin. Principiul maxim al lui Pontryagin este discutat mai detaliat în carte.

Unde este folosit?

Principiul maxim este deosebit de important în sistemele de control cu ​​viteză maximă și consum minim de energie, unde sunt utilizate comenzi de tip releu care iau valori extreme mai degrabă decât intermediare în intervalul de control permis.

Poveste

Pentru dezvoltarea teoriei controlului optim L.S. Pontryagin și colaboratorii săi V.G. Boltyansky, R.V. Gamkrelidze și E.F. Mișcenko a primit Premiul Lenin în 1962.

Metoda de programare dinamică

Metoda de programare dinamică se bazează pe principiul optimității lui Bellman, care se formulează astfel: strategia optimă de control are proprietatea că indiferent de starea inițială și de control la începutul procesului, controalele ulterioare trebuie să constituie o strategie de control optimă în raport cu starea obținută după etapa inițială a procesului. Metoda de programare dinamică este descrisă mai detaliat în carte

Note

Literatură

1. Rastrigin L.A. Principii moderne de gestionare a obiectelor complexe. - M.: Sov. radio, 1980. - 232 p., BBK 32.815, ref. 12000 de exemplare
2. Alekseev V.M., Tikhomirov V.M. , Fomin S.V. Control optim. - M.: Nauka, 1979, UDC 519,6, - 223 p., liniuță. 24000 de exemplare

Vezi de asemenea

Fundația Wikimedia.

2010.

Control optim Vedeți ce înseamnă „Control optim” în alte dicționare: - OU Control care oferă cea mai favorabilă valoare a unui anumit criteriu de optimitate (OC), care caracterizează eficacitatea controlului sub anumite restricții. Diverse tehnice sau economice... ...

Dicționar-carte de referință de termeni ai documentației normative și tehnice control optim - Management, al cărui scop este asigurarea valorii extreme a indicatorului de calitate a managementului. [Culegere de termeni recomandați. Problema 107. Teoria managementului. Academia de Științe a URSS. Comitetul de terminologie științifică și tehnică. 1984]……

Control optim Ghidul tehnic al traducătorului - 1. Conceptul de bază al teoriei matematice a proceselor optime (aparținând ramului matematicii sub același nume: „O.u.”); înseamnă selecția parametrilor de control care ar oferi cel mai bun din punctul de vedere al... ...

Permite, în condiții date (adesea contradictorii), atingerea scopului în cel mai bun mod posibil, de exemplu. in timp minim, cu cel mai mare efect economic, cu maxima acuratete... Dicţionar enciclopedic mare

Aeronava este o secțiune a dinamicii zborului dedicată dezvoltării și utilizării metodelor de optimizare pentru a determina legile de control al mișcării aeronavei și a traiectoriilor acesteia care oferă maximul sau minimul criteriului selectat... ... Enciclopedia tehnologiei

O ramură a matematicii care studiază probleme variaționale non-clasice. Obiectele cu care se ocupă tehnologia sunt de obicei echipate cu „cârme” cu ajutorul lor, o persoană controlează mișcarea. Matematic, comportamentul unui astfel de obiect este descris... ... Marea Enciclopedie Sovietică

Sistemele de control automate optime sunt sisteme în care controlul se realizează în așa fel încât criteriul de optimitate cerut să aibă o valoare extremă. Condiții de limită care definesc stările inițiale și finale necesare ale sistemului; tн Se stabilește în cazurile în care abaterea medie pe un anumit interval de timp prezintă un interes deosebit și sarcina sistemului de control este să asigure un minim din această integrală...

Dacă această lucrare nu vă convine, în partea de jos a paginii există o listă cu lucrări similare. De asemenea, puteți utiliza butonul de căutare

Control optim

Voronov A.A., Titov V.K., Novogranov B.N. Fundamentele teoriei reglării și controlului automat. M.: Şcoala superioară, 1977. 519 p. p. 477 491.

Pistoale autopropulsate optime acestea sunt sisteme în care controlul se realizează în aşa fel încât criteriul de optimitate cerut să aibă o valoare extremă.

Exemple de management optim al obiectelor:

1. Controlul mișcării unei rachete pentru a atinge o înălțime sau o rază de acțiune dată cu un consum minim de combustibil;
2. Controlul mișcării unui mecanism acționat de un motor, ceea ce ar minimiza costurile cu energie;
3. Controlul unui reactor nuclear pentru performanță maximă.

Problema de control optim este formulată după cum urmează:

„Găsiți o astfel de lege a schimbării în timpul de control u(t ), în care sistemul, sub anumite restricții, se va muta de la o stare dată la alta într-un mod optim în sensul că funcțional eu , exprimând calitatea procesului, va primi o valoare extremă”.

Pentru a rezolva problema de control optim, trebuie să știți:

1. Descrierea matematică a obiectului și a mediului, conectând valorile tuturor coordonatelor procesului studiat, controlul și influențele perturbatoare;

2. Restricții fizice asupra coordonatelor și legii de control, exprimate matematic;

3. Condiții la limită care definesc stările inițiale și finale necesare ale sistemului

(scopul tehnologic al sistemului);

4. Funcția obiectivă (funcțională de calitate

scop matematic).

Din punct de vedere matematic, criteriul de optimitate este cel mai adesea prezentat astfel:

t la

I =∫ f o [ y (t), u (t), f (t), t ] dt + φ [ y (t la), t la ], (1)

t n

unde primul termen caracterizează calitatea controlului pe întreg intervalul ( tn, tn) și se numește

componentă integrală, al doilea termen

caracterizează precizia la momentul final (terminal) în timp t la .

Expresia (1) se numește funcțională, deoarece eu depinde de alegerea funcției u(t ) și rezultatul y(t).

Problema Lagrange.Minimizează funcționalitatea

t la

I=∫f o dt.

t n

Este utilizat în cazurile în care abaterea medie în timp prezintă un interes deosebit.

un anumit interval de timp, iar sarcina sistemului de control este de a asigura un minim din această integrală (deteriorarea calității produsului, pierdere etc.).

Exemple de funcționalitate:

I =∫ (t) dt criteriu pentru eroare minimă în regim stabil, unde x(t)

1. abaterea parametrului controlat de la valoarea specificată;

I =∫ dt = t 2 - t 1 = > min criteriul pentru viteza maximă a tunurilor autopropulsate;

I =∫ dt => min criteriul eficienţei optime.

problema lui Mayer. În acest caz, funcționalitatea care este minimizată este cea definită doar de partea terminală, adică.

I = φ =>min.

De exemplu, pentru un sistem de control al aeronavei descris de ecuație

F o (x, u, t),

puteți seta următoarea sarcină: determinați controlul u (t), t n ≤ t ≤ t k astfel încât pentru

timpul de zbor dat pentru a atinge intervalul maxim, cu condiția ca în momentul final al timpului t la Aeronava va ateriza, adică x (t la ) =0.

Problema Boltz se reduce la problema minimizării criteriului (1).

Metodele de bază pentru rezolvarea problemelor de control optim sunt:

1.Calcul clasic al variațiilor Teorema și ecuația lui Euler;

2. Principiul L.S. maxim. Pontryagin;

3.Programare dinamică de R. Bellman.

ECUAȚIA ȘI TEOREMA LUI EULER

Să fie dată funcționalitatea:

t la

I =∫ f o dt ,

t n

Unde unele funcții de două ori diferențiabile, printre care este necesar să se găsească astfel de funcții ( t ) sau extremale , care îndeplinesc condițiile la limită specificate x i (t n), x i (t k ) și minimizați funcționalitatea.

Extremele se găsesc printre soluțiile ecuației lui Euler

eu = .

Pentru a stabili faptul de a minimiza funcționalitatea, este necesar să ne asigurăm că condițiile Lagrange sunt îndeplinite de-a lungul extremelor:

similar cu cerințele pentru pozitivitatea derivatei a doua în punctul minim al funcției.

teorema lui Euler: „Dacă extremul funcționalului eu există și se realizează printre curbele netede, atunci poate fi realizat doar pe extreme.”

PRINCIPIUL MAXIM AL L.S.PONTRYAGIN

Școala lui L.S Pontryagin a formulat o teoremă despre condiția necesară a optimității, a cărei esență este următoarea.

Să presupunem că ecuația diferențială a obiectului, împreună cu partea neschimbabilă a dispozitivului de control, este dată în forma generală:

Pentru a vă controla j restricțiile pot fi impuse, de exemplu, sub formă de inegalități:

, .

Scopul controlului este de a transfera obiectul din starea inițială ( t n ) la starea finală ( t la ). Momentul final al procesului t la poate fi fix sau gratuit.

Fie criteriul optimității minimul funcționalității

I = dt.

Să introducem variabile auxiliare și să formăm o funcție

Fo ()+ f () f ()+

Principiul maximului prevede că pentru ca sistemul să fie optim, adică. pentru a obține minimul funcționalului, este necesar să existe astfel de funcții continue non-nule care să satisfacă ecuația

Asta pentru orice t , situat într-un interval dat t n≤ t ≤ t k , valoarea lui H, în funcție de controlul admisibil, atinge un maxim.

Maximul funcției H este determinat din condițiile:

daca nu ajunge la limitele regiunii, iar ca suprema functiei H, in caz contrar.

Programare dinamică de R. Bellman

Principiul optimității lui R. Bellman:

„Comportamentul optim are proprietatea că, indiferent de starea și decizia inițială la momentul inițial, deciziile ulterioare trebuie să constituie un comportament optim în raport cu starea rezultată din prima decizie.”

„Comportamentul” sistemului trebuie înțeles circulaţie aceste sisteme și termenul„decizie” se referă laalegerea legii schimbării în timp a forţelor de control.

În programarea dinamică, procesul de căutare a extremelor este împărțit în n pași, în timp ce în calculul clasic al variațiilor se efectuează căutarea întregului extremal.

Procesul de căutare a unui extremal se bazează pe următoarele premise ale principiului optimității lui R. Bellman:

1. Fiecare segment al traiectoriei optime este el însuși o traiectorie optimă;
2. Procesul optim la fiecare sit nu depinde de istoricul acestuia;
3. Controlul optim (traiectoria optimă) este căutat folosind mișcarea înapoi [de la y (T) la y (T -∆), unde ∆ = T/ N, N numărul de secțiuni ale traiectoriei etc.].

Din punct de vedere euristic, ecuațiile Bellman pentru enunțurile problemei necesare sunt derivate pentru sisteme continue și discrete.

Control adaptiv

Andrievsky B.R., Fradkov A.L. Capitole selectate de teoria controlului automat cu exemple în limbaj MATLAB . Sankt Petersburg: Nauka, 1999. 467 p. Capitolul 12.

Voronov A.A., Titov V.K., Novogranov B.N. Fundamentele teoriei reglării și controlului automat. M.: Şcoala superioară, 1977. 519 p. p. 491 499.

Ankhimyuk V.L., Opeiko O.F., Mikheev N.N. Teoria controlului automat. Mn.: Design PRO, 2000. 352 p. p. 328 340.

Necesitatea sistemelor de control adaptive apare din cauza complicației semnificative a problemelor de control care se rezolvă, iar o caracteristică specifică a acestei complicații este lipsa oportunității practice pentru un studiu și descriere detaliată a proceselor care au loc în obiectul controlat.

De exemplu, aeronavele moderne de mare viteză, date precise a priori ale căror caracteristici în toate condițiile de operare nu pot fi obținute din cauza variațiilor semnificative ale parametrilor atmosferici, gamelor mari de viteze de zbor, intervale și altitudini, precum și datorită prezenței a unei game largi de perturbaţii parametrice şi externe.

Unele obiecte de control (avioane și rachete, procese tehnologice și centrale electrice) se disting prin faptul că caracteristicile lor statice și dinamice se modifică într-o gamă largă într-un mod care nu a fost anticipat în prealabil. Gestionarea optimă a unor astfel de obiecte este posibilă cu ajutorul sistemelor în care informațiile lipsă sunt completate automat de sistemul însuși în timpul funcționării.

Adaptiv (lat.) adaptio ”dispozitiv) sunt acele sisteme care, la modificarea parametrilor obiectelor sau a caracteristicilor influențelor externe în timpul funcționării, în mod independent, fără intervenția omului, modifică parametrii regulatorului, structura acestuia, setările sau influențele de reglementare pentru a menține modul optim de funcționare al obiectul.

Crearea sistemelor de control adaptiv se realizează în condiții fundamental diferite, adică metodele adaptative ar trebui să ajute la realizarea unui control de înaltă calitate în absența unei completități suficiente a informațiilor a priori despre caracteristicile procesului controlat sau în condiții de incertitudine.

Clasificarea sistemelor adaptive:

Autoadaptare

(adaptativ)

Sisteme de control

Sisteme de auto-învățare cu autoajustare cu adaptare

Sisteme de sisteme în faze speciale

state

Căutare fără căutare- Training- Training- Relay Adaptive

(extrem (analizat cu stimulente fără sistem de auto-oscilare cu

Noi) variabile de stimulare tic

Structura sistemelor sistemelor

Diagrama structurală a clasificării AS (în funcție de natura procesului de adaptare)

Sisteme de autoajustare (SNS)sunt sisteme în care adaptarea la condițiile de funcționare în schimbare se realizează prin modificarea parametrilor și acțiunile de control.

Auto-organizareAcestea sunt sisteme în care adaptarea se realizează prin modificarea nu numai a parametrilor și acțiunilor de control, ci și a structurii.

Auto-învățareacesta este un sistem de control automat în care modul optim de funcționare al obiectului controlat este determinat folosind un dispozitiv de control, al cărui algoritm este îmbunătățit automat în mod intenționat în procesul de învățare prin căutare automată. Căutarea se efectuează folosind un al doilea dispozitiv de control, care este o parte organică a sistemului de auto-învățare.

În motoarele de căutare sisteme, modificarea parametrilor dispozitivului de control sau acțiunea de control se efectuează ca urmare a căutării condițiilor pentru extremul indicatorilor de calitate. Căutarea condițiilor extreme în sistemele de acest tip se realizează folosind influențe de testare și evaluarerezultate obţinute.

În non-căutare sisteme, determinarea parametrilor dispozitivului de control sau a acțiunilor de control se realizează pe baza determinării analitice a condițiilor care asigură calitatea specificată a controlului fără utilizarea semnalelor speciale de căutare.

Sisteme cu adaptare în stări de fază specialăutilizați moduri sau proprietăți speciale ale sistemelor neliniare (moduri de auto-oscilație, moduri de alunecare) pentru a organiza modificări controlate ale proprietăților dinamice ale sistemului de control. Moduri speciale organizate special în astfel de sisteme fie servesc ca o sursă suplimentară de informații operaționale despre condițiile de funcționare în schimbare ale sistemului, fie dotează sistemele de control cu ​​noi proprietăți, datorită cărora caracteristicile dinamice ale procesului controlat sunt menținute în limitele dorite. , indiferent de natura modificărilor care apar în timpul funcționării.

Când se utilizează sisteme adaptive, sunt rezolvate următoarele sarcini principale:

1 . În timpul funcționării sistemului de control, când parametrii, structura și influențele externe se modifică, este asigurat un control în care sunt menținute proprietățile dinamice și statice specificate ale sistemului;

2 . În timpul procesului de proiectare și punere în funcțiune, în absența inițială a informațiilor complete despre parametrii, structura obiectului de control și influențele externe, sistemul este ajustat automat în conformitate cu proprietățile dinamice și statice specificate.

Exemplul 1 . Sistem adaptiv de stabilizare a poziției unghiulare a aeronavei.

f 1 (t) f 2 (t) f 3 (t)

D1 D2 D3

VU1 VU2 VU3 f (t) f 1 (t) f 2 (t) f 3 (t)

u (t) W 1 (p) W 0 (p) y (t)

+ -

Orez. 1.

Sistem adaptiv de stabilizare a aeronavei

Când condițiile de zbor se schimbă, funcția de transfer se schimbă W 0 (pag ) aeronave și, în consecință, caracteristicile dinamice ale întregului sistem de stabilizare:

. (1)

Tulburări din mediul extern f 1 (t), f 2 (t), f 3 (t ) care conduc la modificări controlate ale parametrilor sistemului sunt aplicate în diferite puncte ale obiectului.

Influență tulburătoare f(t ) aplicat direct la intrarea obiectului de control, spre deosebire de f 1 (t), f 2 (t), f 3 (t ) nu își modifică parametrii. Prin urmare, în timpul funcționării sistemului, numai f 1 (t), f 2 (t), f 3 (t).

În conformitate cu principiul feedback-ului și expresia (1), modificări necontrolate ale caracteristicilor W 0 (pag ) din cauza perturbațiilor și interferențelor provoacă modificări relativ mici ale parametrilor Ф( p) .

Dacă stabilim sarcina unei compensări mai complete a modificărilor controlate, astfel încât funcția de transfer Ф(р) a sistemului de stabilizare a aeronavei să rămână practic neschimbată, atunci caracteristicile controlerului ar trebui modificate în mod corespunzător W 1 (pag ). Acest lucru se realizează într-un pistol autopropulsat adaptabil, realizat conform schemei din Fig. 1. Parametri de mediu caracterizați prin semnale f 1 (t), f 2 (t), f 3 (t ), de exemplu, presiunea de cap de viteză P H(t) , temperatura mediului ambiant T0(t) și viteza de zbor v(t) , sunt măsurate continuu de senzorii D 1, D 2, D 3 , iar valorile actuale ale parametrilor sunt trimise la dispozitivele de calcul B 1, B 2, B 3 , producând semnale cu ajutorul cărora se reglează caracteristica W 1 (pag ) pentru a compensa modificările caracteristicilor W0(p).

Cu toate acestea, într-un sistem de control automat de acest tip (cu o buclă de configurare deschisă) nu există o autoanaliză a eficacității modificărilor controlate pe care le face.

Exemplul 2. Sistemul de control al vitezei de zbor extreme a aeronavei.

Z Perturbare

Impact

X 3 = X 0 - X 2

Dispozitiv automat X 0 Amplificare X 4 Executive X 5 Ajustabil X 1

Obiect dispozitiv convertor matematic

Extremum iska + - dispozitiv

Măsurare

Dispozitiv

Fig. 2. Schema funcțională a unui sistem de control al vitezei de zbor extreme a aeronavei

Sistemul extremal determină cel mai profitabil program, adică. apoi valoarea X 1 (viteza necesara a aeronavei), care trebuie mentinuta in acest moment pentru a produce un consum minim de combustibil pe unitatea de lungime a traiectoriei.

Z - caracteristicile obiectului; X 0 - influenţa controlului asupra sistemului.

(valoarea consumului de combustibil)

y(0)

y(T)

Sisteme de auto-organizare