Determinați intervalul de încredere al valorii medii. Interval de încredere pentru așteptările matematice

Pentru marea majoritate a măsurătorilor simple, așa-numita lege normală a erorilor aleatoare este satisfăcută destul de bine ( legea lui Gauss), derivat din următoarele prevederi empirice.

1) erorile de măsurare pot lua o serie continuă de valori;

2) cu un număr mare de măsurători, erori de aceeași amploare, dar de semne diferite, apar la fel de des,

3) cu cât este mai mare magnitudinea erorii aleatorii, cu atât este mai puțin probabil să apară.

Graficul legii distribuției gaussiene normale este prezentat în Fig. 1. Ecuația curbei este

unde este funcția de distribuție a erorilor aleatoare (erori), care caracterizează probabilitatea unei erori, σ este eroarea pătratică medie.

Mărimea σ nu este o variabilă aleatoare și caracterizează procesul de măsurare. Dacă condițiile de măsurare nu se schimbă, atunci σ rămâne o valoare constantă. Pătratul acestei mărimi se numește dispersie de măsurare. Cu cât dispersia este mai mică, cu atât răspândirea valorilor individuale este mai mică și precizia măsurării este mai mare.

Valoarea exactă a erorii pătratice medii σ, precum și valoarea adevărată a valorii măsurate, sunt necunoscute. Există o așa-numită estimare statistică a acestui parametru, conform căreia eroarea pătratică medie este egală cu eroarea pătratică medie a mediei aritmetice. A cărui valoare este determinată de formula

unde este rezultatul i a-a dimensiune; - media aritmetică a valorilor obţinute; n– numărul de măsurători.

Cu cât este mai mare numărul de dimensiuni, cu atât este mai mic și se apropie de σ. Dacă valoarea adevărată a mărimii măsurate este μ, valoarea medie aritmetică a acesteia obținută în urma măsurătorilor este , iar eroarea absolută aleatorie este , atunci rezultatul măsurării va fi scris sub forma .

Se numește intervalul de valori de la până la , care conține valoarea adevărată a mărimii măsurate μ interval de încredere. Deoarece este o variabilă aleatoare, valoarea adevărată se încadrează în intervalul de încredere cu probabilitatea α, care se numește probabilitatea de încredere, sau fiabilitate măsurători. Această valoare este numeric egală cu aria trapezului curbat umbrit. (vezi poza)

Toate acestea sunt valabile pentru un număr suficient de mare de măsurători, când σ este aproape. Pentru a găsi intervalul de încredere și probabilitatea de încredere pentru un număr mic de măsurători, de care ne ocupăm în cursul lucrărilor de laborator, folosim Distribuția probabilității elevilor. Aceasta este distribuția de probabilitate a unei variabile aleatoare numite Coeficientul elevului, dă valoarea intervalului de încredere în fracții din eroarea pătratică medie a mediei aritmetice.

Distribuția de probabilitate a acestei mărimi nu depinde de σ 2, dar depinde semnificativ de numărul de experimente n. Odată cu creșterea numărului de experimente n distribuția Student tinde către distribuția Gauss.

Funcția de distribuție este tabelată (Tabelul 1). Valoarea coeficientului Student se află la intersecția dreptei corespunzătoare numărului de măsurători n, iar coloana corespunzătoare probabilității de încredere α

Se numește probabilitatea ca adevărata valoare a mărimii măsurate să se afle într-un anumit interval probabilitatea de încredere , sau coeficient de fiabilitate, și intervalul în sine - interval de încredere.

Fiecare probabilitate de încredere are propriul interval de încredere. În special, un nivel de încredere de 0,67 corespunde unui interval de încredere de la până la . Cu toate acestea, această afirmație este adevărată numai pentru un număr suficient de mare de măsurători (mai mult de 10), iar probabilitatea de 0,67 nu pare suficient de fiabilă - în aproximativ fiecare dintre cele trei serii de măsurători y poate fi în afara intervalului de încredere. Pentru a obține o mai mare încredere că valoarea valorii măsurate se află în intervalul de încredere, se stabilește de obicei o probabilitate de încredere de 0,95 - 0,99. Interval de încredere pentru o probabilitate de încredere dată, ținând cont de influența numărului de măsurători n poate fi găsit prin înmulțirea abaterii standard a mediei aritmetice

.

prin așa-numitul coeficient Student. Coeficienții elevului pentru o serie de valori și n sunt date în tabel.

Tabel - Coeficienții elevilor

În sfârșit, pentru cantitatea măsurată y pentru o probabilitate de încredere dată y și numărul de măsurători n primim starea

Vom chema cantitatea eroare aleatorie cantități y.

Exemplu: vezi prelegerea nr. 5 – o serie de numere.

Să definim

Cu un număr de măsurători de 45 și o probabilitate de încredere de 0,95, obținem că coeficientul Student este aproximativ egal cu 2,15. Atunci intervalul de încredere pentru această serie de măsurători este 62,6.

Ratări (eroare gravă) - erori grosolane datorate erorilor operatorului sau nesocotite influente externe. Acestea sunt de obicei excluse din rezultatele măsurătorilor. Greșelile sunt de obicei cauzate de neatenție. Ele pot apărea și din cauza unei defecțiuni a dispozitivului.

Notează sarcina. De exemplu: Greutatea medie a unui student de sex masculin la Universitatea ABC este de 90 kg. Veți testa acuratețea predicției ponderii studenților de sex masculin de la Universitatea ABC într-un interval de încredere dat.

Selectați o probă potrivită.Îl vei folosi pentru a colecta date pentru a-ți testa ipoteza. Să presupunem că ați selectat deja aleatoriu 1000 de studenți bărbați.

Calculați media și abaterea standard a acestui eșantion. Selecta mărimi statistice(cum ar fi media și abaterea standard) pe care doriți să le utilizați pentru a analiza proba. Iată cum se calculează media și abaterea standard:

• Pentru a calcula media eșantionului, adunați greutățile celor 1.000 de bărbați eșantionați și împărțiți rezultatul la 1.000 (numărul de bărbați). Să presupunem că obținem o greutate medie de 93 kg.
• Pentru a calcula abaterea standard a unui eșantion, trebuie să găsiți media. Apoi trebuie să calculați varianța datelor sau media diferențelor pătrate față de medie. Odată ce găsiți acest număr, luați pur și simplu rădăcina pătrată a acestuia. Să presupunem că în exemplul nostru abaterea standard este de 15 kg (rețineți că uneori această informație poate fi dată împreună cu condițiile problemei statistice).

Interval de încredere pentru așteptările matematice - acesta este un interval calculat din date care, cu o probabilitate cunoscuta, contine asteptarea matematica a populatiei generale. O estimare naturală pentru așteptarea matematică este media aritmetică a valorilor observate. Prin urmare, pe parcursul lecției vom folosi termenii „medie” și „valoare medie”. În problemele de calculare a unui interval de încredere, un răspuns solicitat cel mai adesea este ceva de genul „Intervalul de încredere al mediei [valoarea unei anumite probleme] este de la [valoarea mai mică] la [valoarea mai mare]”. Folosind un interval de încredere, puteți evalua nu numai valorile medii, ci și proporția unei anumite caracteristici a populației generale. Valorile medii, dispersia, abaterea standard și eroarea, prin care vom ajunge la noi definiții și formule, sunt discutate în lecție Caracteristicile eșantionului și populației .

Estimări punctuale și pe intervale ale mediei

Dacă valoarea medie a populației este estimată printr-un număr (punct), atunci o medie specifică, care este calculată dintr-un eșantion de observații, este luată ca o estimare a valorii medii necunoscute a populației. În acest caz, valoarea mediei eșantionului - o variabilă aleatorie - nu coincide cu valoarea medie a populației generale. Prin urmare, atunci când indicați media eșantionului, trebuie să indicați simultan eroarea de eșantionare. Măsura erorii de eșantionare este eroarea standard, care este exprimată în aceleași unități ca și media. Prin urmare, se folosește adesea următoarea notație: .

Dacă estimarea mediei trebuie să fie asociată cu o anumită probabilitate, atunci parametrul de interes în populație trebuie estimat nu printr-un număr, ci printr-un interval. Un interval de încredere este un interval în care, cu o anumită probabilitate P se constată valoarea indicatorului populaţiei estimate. Interval de încredere în care este probabil P = 1 - α se găsește variabila aleatoare, calculată după cum urmează:

,

α = 1 - P, care poate fi găsit în anexa la aproape orice carte de statistică.

În practică, media și varianța populației nu sunt cunoscute, astfel încât varianța populației este înlocuită cu varianța eșantionului, iar media populației cu media eșantionului. Astfel, intervalul de încredere în majoritatea cazurilor se calculează după cum urmează:

.

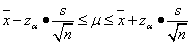Formula intervalului de încredere poate fi utilizată pentru a estima media populației dacă

• se cunoaște abaterea standard a populației;
• sau abaterea standard a populației este necunoscută, dar dimensiunea eșantionului este mai mare de 30.

Media eșantionului este o estimare imparțială a mediei populației. La rândul său, varianța eșantionului nu este o estimare imparțială a varianței populației. Pentru a obține o estimare imparțială a varianței populației în formula variației eșantionului, dimensiunea eșantionului n ar trebui înlocuit cu n-1.

Exemplul 1. S-au colectat informații din 100 de cafenele selectate aleatoriu dintr-un anumit oraș că numărul mediu de angajați din acestea este de 10,5 cu o abatere standard de 4,6. Determinați intervalul de încredere de 95% pentru numărul de angajați ai cafenelei.

unde este valoarea critică a distribuției normale standard pentru nivelul de semnificație α = 0,05 .

Astfel, intervalul de încredere de 95% pentru numărul mediu de angajați ai cafenelei a variat între 9,6 și 11,4.

Exemplul 2. Pentru un eșantion aleatoriu din populația de 64 de observații, au fost calculate următoarele valori totale:

suma valorilor din observații,

suma abaterilor pătrate ale valorilor de la medie .

Calculați intervalul de încredere de 95% pentru așteptările matematice.

Să calculăm abaterea standard:

,

Să calculăm valoarea medie:

.

Înlocuim valorile în expresia pentru intervalul de încredere:

unde este valoarea critică a distribuției normale standard pentru nivelul de semnificație α = 0,05 .

Primim:

Astfel, intervalul de încredere de 95% pentru așteptarea matematică a acestui eșantion a variat între 7,484 și 11,266.

Exemplul 3. Pentru un eșantion de populație aleatoriu de 100 de observații, media calculată este 15,2 și abaterea standard este 3,2. Calculați intervalul de încredere de 95% pentru valoarea așteptată, apoi intervalul de încredere de 99%. Dacă puterea eșantionului și variația acesteia rămân neschimbate și coeficientul de încredere crește, intervalul de încredere se va îngusta sau se va lărgi?

Inlocuim aceste valori in expresia pentru intervalul de incredere:

unde este valoarea critică a distribuției normale standard pentru nivelul de semnificație α = 0,05 .

Primim:

.

Astfel, intervalul de încredere de 95% pentru media acestui eșantion a variat între 14,57 și 15,82.

Substituim din nou aceste valori în expresia pentru intervalul de încredere:

unde este valoarea critică a distribuției normale standard pentru nivelul de semnificație α = 0,01 .

Primim:

.

Astfel, intervalul de încredere de 99% pentru media acestui eșantion a variat între 14,37 și 16,02.

După cum vedem, pe măsură ce coeficientul de încredere crește, crește și valoarea critică a distribuției normale standard și, în consecință, punctele de început și de sfârșit ale intervalului sunt situate mai departe de medie și astfel intervalul de încredere pentru așteptarea matematică crește. .

Estimări punctiforme și pe intervale ale greutății specifice

Ponderea unui atribut al eșantionului poate fi interpretată ca o estimare punctuală a cotei p de aceeaşi caracteristică în populaţia generală. Dacă această valoare trebuie să fie asociată cu probabilitatea, atunci intervalul de încredere al greutății specifice trebuie calculat p caracteristică în populaţie cu probabilitate P = 1 - α :

.

Exemplul 4.Într-un oraș sunt doi candidați OŞi B candideaza pentru functia de primar. 200 de locuitori ai orașului au fost chestionați aleatoriu, dintre care 46% au răspuns că ar vota pentru candidat O, 26% - pentru candidat B iar 28% nu știu pe cine vor vota. Determinați intervalul de încredere de 95% pentru proporția de locuitori ai orașului care susțin candidatul O.

Konstantin Kravchik explică clar ce este un interval de încredere în cercetarea medicală și cum să-l folosească

„Katren-Style” continuă publicarea ciclului lui Konstantin Kravchik despre statistici medicale. În două articole anterioare, autorul s-a ocupat de explicarea unor concepte precum și.

Constantin Kravcik

Matematician-analist. Specialist în cercetare statistică în medicină și științe umaniste

Oraș: Moscova

Foarte des în articolele despre studii clinice puteți găsi o frază misterioasă: „interval de încredere” (95 % CI sau 95 % CI - interval de încredere). De exemplu, un articol ar putea scrie: „Pentru a evalua semnificația diferențelor, a fost folosit testul t Student pentru a calcula intervalul de încredere de 95 %”.

Care este valoarea „intervalului de încredere 95 %” și de ce să-l calculăm?

Ce este un interval de încredere? - Acesta este intervalul în care adevărata populație înseamnă minciună. Există medii „neadevărate”? Într-un fel, da, o fac. În am explicat că este imposibil să se măsoare parametrul de interes în întreaga populație, așa că cercetătorii se mulțumesc cu un eșantion limitat. În această probă (de exemplu, după greutatea corporală) există o valoare medie (o anumită greutate), după care judecăm valoarea medie în întreaga populație. Cu toate acestea, este puțin probabil ca greutatea medie dintr-un eșantion (în special unul mic) să coincidă cu ponderea medie în populația generală. Prin urmare, este mai corect să se calculeze și să se utilizeze intervalul de valori medii ale populației.

De exemplu, imaginați-vă că intervalul de încredere de 95% (IC 95%) pentru hemoglobină este de 110 până la 122 g/L. Aceasta înseamnă că există o șansă de 95% ca valoarea medie reală a hemoglobinei în populație să fie între 110 și 122 g/L. Cu alte cuvinte, nu cunoaștem valoarea medie a hemoglobinei în populație, dar putem, cu o probabilitate de 95 %, să indicăm o gamă de valori pentru această trăsătură.

Intervalele de încredere sunt deosebit de relevante pentru diferențele de medii între grupuri sau mărimea efectului, așa cum sunt numite.

Să presupunem că am comparat eficiența a două preparate de fier: unul care este pe piață de mult timp și unul care tocmai a fost înregistrat. După cursul terapiei, am evaluat concentrația de hemoglobină în loturile de pacienți studiate, iar programul statistic a calculat că diferența dintre valorile medii ale celor două loturi a fost, cu o probabilitate de 95 %, în intervalul de la 1,72 la 14,36 g/l (Tabelul 1).

Masă 1. Testare pentru mostre independente
(grupurile sunt comparate în funcție de nivelul hemoglobinei)

Acest lucru ar trebui interpretat după cum urmează: la unii pacienți din populația generală care iau un medicament nou, hemoglobina va fi mai mare în medie cu 1,72-14,36 g/l decât la cei care au luat un medicament deja cunoscut.

Cu alte cuvinte, în populația generală, diferența de valori medii ale hemoglobinei între grupuri este în aceste limite cu o probabilitate de 95%. Va rămâne la latitudinea cercetătorului să judece dacă este mult sau puțin. Ideea tuturor acestor lucruri este că nu lucrăm cu o valoare medie, ci cu o gamă de valori, prin urmare, estimăm mai fiabil diferența unui parametru între grupuri.

În pachetele statistice, la discreția cercetătorului, puteți îngusta sau extinde în mod independent granițele intervalului de încredere. Prin scăderea probabilităților intervalului de încredere, restrângem intervalul de medii. De exemplu, la 90 % CI intervalul de medii (sau diferența de medii) va fi mai restrâns decât la 95 %.

În schimb, creșterea probabilității la 99 % extinde gama de valori. Când se compară grupuri, limita inferioară a CI poate depăși marcajul zero. De exemplu, dacă am extins limitele intervalului de încredere la 99 %, atunci limitele intervalului au variat între –1 și 16 g/l. Aceasta înseamnă că în populația generală există grupuri, diferența de medii între care pentru caracteristica studiată este egală cu 0 (M = 0).

Folosind un interval de încredere, puteți testa ipotezele statistice. Dacă intervalul de încredere depășește valoarea zero, atunci ipoteza nulă, care presupune că grupurile nu diferă în funcție de parametrul studiat, este adevărată. Exemplul este descris mai sus în care am extins limitele la 99 %. Undeva în populația generală am găsit grupuri care nu diferă în niciun fel.

Interval de încredere de 95% al ​​diferenței de hemoglobină, (g/l)

Figura arată intervalul de încredere de 95% pentru diferența dintre valorile medii ale hemoglobinei dintre cele două grupuri. Linia trece prin marcajul zero, prin urmare există o diferență între mediile lui zero, ceea ce confirmă ipoteza nulă că grupurile nu diferă. Intervalul de diferență între grupuri este de la –2 la 5 g/L. Aceasta înseamnă că hemoglobina poate fie să scadă cu 2 g/L, fie să crească cu 5 g/L.

Intervalul de încredere este un indicator foarte important. Datorită acesteia, puteți vedea dacă diferențele dintre grupuri s-au datorat într-adevăr diferenței de medii sau datorită unui eșantion mare, deoarece la un eșantion mare șansele de a găsi diferențe sunt mai mari decât la unul mic.

În practică ar putea arăta așa. Am luat un eșantion de 1000 de persoane, am măsurat nivelurile de hemoglobină și am constatat că intervalul de încredere pentru diferența de medii a variat între 1,2 și 1,5 g/l. Nivelul semnificației statistice în acest caz p

Vedem că concentrația de hemoglobină a crescut, dar aproape imperceptibil, prin urmare, semnificația statistică a apărut tocmai datorită dimensiunii eșantionului.

Intervalele de încredere pot fi calculate nu numai pentru medii, ci și pentru proporții (și rapoarte de risc). De exemplu, ne interesează intervalul de încredere al proporțiilor de pacienți care au obținut remisie în timp ce luau un medicament dezvoltat. Să presupunem că 95 % CI pentru proporții, adică pentru proporția de astfel de pacienți, se află în intervalul 0,60-0,80. Astfel, putem spune că medicamentul nostru are un efect terapeutic în 60 până la 80 % din cazuri.